Distance Calculation
The focus here is on determining how far apart two points are in
terms of their coordinates, features, or representations.
Distance measures are always non-negative and are usually
symmetric (i.e., the distance from point A to point B is the
same as the distance from point B to point A).
What methods can we use?
2D space:
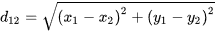
Full space:

Standardized Euclidean distance
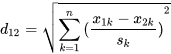
2D space:
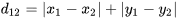
Full space:

2D space:

Full space:
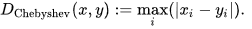
2D space:
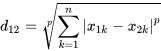
Full space:
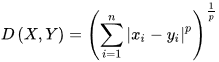
In information theory, the Hamming distance between two strings of equal length is the number of positions at which the corresponding symbols are different. In other words, it measures the minimum number of substitutions required to change one string into the other, or the minimum number of errors that could have transformed one string into the other.
