Greedy Algorithms
- The change-making problem addresses the question of finding
the minimum number of coins (of certain denominations) that add
up to a given amount of money.
Given unlimited amounts of coins of denominations d1 > … > dm , give change for amount n with the least number of coins.
- "Normal" Coin change problem: d1 = 25c, d2 =10c, d3 = 5c, d4 = 1c and n = 48c (How about n=90c?)
- Knapsack problem: Given a set of items, each with a weight and a value, determine which items to include in the collection so that the total weight is less than or equal to a given limit and the total value is as large as possible.

- Can you design a Greedy Algorithm to find the best solution?
- Can you find a test case as a counter-example for your algorithm?
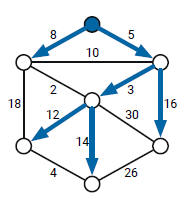
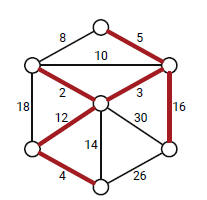
- Spanning tree of a connected graph G: a connected acyclic
subgraph of G that includes all of G’s vertices
Minimum spanning tree of a weighted, connected graph G: a spanning tree of G of minimum total weight
- Single Source Shortest Paths Problem: Given a weighted connected graph G, find shortest paths from source vertex s to each of the other vertices