resources:
graphsketch.com
(notation: 'lg' denotes log_2 and 'log' denotes log_10 unless otherwise noted.)
Asymptotics in computer science is the foundation of big-oh notation, which is the method by which functions, generally those that model algorithms, are compared to each other. The *big-oh* refers to the uppercase letter Ο (Omicron) in the Greek alphabet.
The function mapping for a function that models an algorithm is N -> N, where N={0,1,2,3,...}. The domain of such functions is generally the size of the input data (e.g., a list of names that need to be sorted). The codomain will be the count of operations performed (e.g., the number of comparison operations that occur in the sort) or the size of space needed to perform the sort (for input n you might need 2n of space). In either case we only need the positive quadrant. These functions are either constant (i.e., f(n) = 100) or increasing (continuing in an upward fashion and never decreasing). Asymptotics allows us to compare two functions f(n) and g(n), where f and g are constant or increasing functions, in terms of their relative growth rate so that we can say whether one function grows faster, more slowly or at the same rate as the other function. The notation to describe the relationship is called big-oh notation:
+ f(n) is big-oh(g(n)) if f(n) grows more slowly or at the same rate as g(n).
+ f(n) is little-o(g(n)) if f(n) grows more slowly than g(n).
+ f(n) is big-Theta(g(n)) if f(n) has the same growth rate as g(n).
+ f(n) is big-Omega(g(n)) if f(n) grows faster or at the same rate as g(n).
From the opposite perspective, if you can say
"f(n) has the same growth rate as g(n)" f(n) is big-Theta(g(n)) or
f(n) is big-oh(g(n)) or
f(n) is big-Omega(g(n)).
"f(n) grows more slowly than g(n)" f(n) is big-oh(g(n)) or
f(n) is little-o(g(n)).
"f(n) grows more rapidly than g(n)" f(n) is big-Omega(g(n).
The typical functions used to compare other functions to, in ascending order of growth rate where each function dominates (grows faster than); i.e., the growth rate is strictly greater than the previous one, are:
1, lg n, n, n lg n, n^2, n^3, 2^n, n!
What does it mean for one function f to grow faster than another function g
in terms of big-oh notation?
It does not mean that if f(n) is always larger than g(n), then f(n) grows
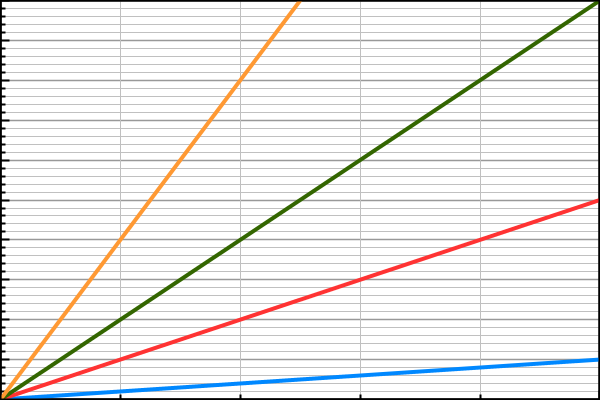
faster. For example, The linear functions f(n)=n (blue),
f(n)=5n (orange), f(n)=10n (green), and f(n)=20n (yellow) are shown
below.
All four functions have a constant growth rate (the change in f(n) over the change in n remains constant). Although f(n) is always larger for 10n than it is for 5n, the functions all have a constant growth rate so are considered to have the same growth rate. How do we know if a function has a faster growth rate than another function? The growth rate of a function must be defined in terms of large values of n. This is where asymptotics comes into play. Asymptotics is the study of limiting behavior of functions over large input; e.g., what happens to f(n) as n approaches infinity? Some examples:
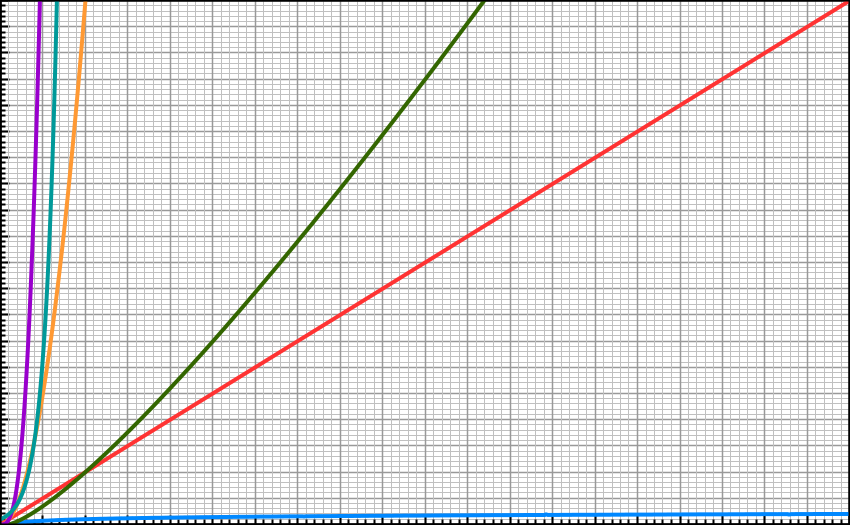
f(x) = 1/x. As x -> oo, f(x) approaches zero. f(x) = x. As x -> oo, f(x) approaches infinity. f(x) = 100. As x -> oo, f(x) = 100.By looking at graphs, we can often clearly see that some functions grow faster than others. This is a graph of log n (blue), n(red), n log n (green), n^2 (yellow), n^3 (teal) and 2^n (purple). We know that n log n (green) has a faster growth rate than n (red) because n log n starts out below n, but very quickly n log n overtakes n. Since all the functions we care about are either constant or are increasing (not both at the same time), we know that once function f overtakes function g that f(n) will always be larger than g(n) after that point.
Now the difficult part is how to tell if one function grows more rapidly, more slowly or at the same rate as another function if you cannot tell by the graph or you cannot easily graph the functions. There are two methods.
METHOD 1. Find a point at which one function overtakes another.
f(n) is O(g(n)) if there exists a C and k such that f(n) <= C g(n) whenever x > k. C and k are called witnesses.For example, assuming C = 1, k is the smallest integer value of n > 1 for which g(n) overtakes f(n):
g(n) f(n) k Conclusion: n^2 15n + 5 16: n^2 = 256, 15n + 5 = 245 15n+5 is O(n^2) 2^n 8 n^4 21: 2^n = 2097152, 8n^4 = 1555848 8n^4 is O(2^n) .1n 10 lg n 997: .1n = 99.7, 10 lgn approx. 99.6 10lgn is O(.1n) lg n lg lg n^2 8: lg n=3 lg lg n^2=1.7 f(n)is O(g(n))Note: the 'C' tells us that we can remove all constants from equations when comparing functions by growth rate.
Method 1 is generally not the way to approach a problem unless you have a good idea that one function dominates another function and you just want to prove it. If you do NOT know which function dominates then you run the risk of thinking you found the solution when, in fact, the number you picked was just not large enough. You really need to use Method 2.
METHOD 2. Find the limit of the ratio of the two functions, as n -> oo.
The limit of f(n)/g(n), n -> oo is either 0, finite and nonzero, or infinity. If the result is
+ 0, then f(n) is strictly smaller than g(n) and the notation is little-oh.
+ finite, then f(n) is smaller or equal to g(n) and the notation is Big-oh.*
+ finite and nonzero, then f(n) is equal to g(n) and the notation is Big Theta.
+ nonzero, then f(n) is larger or equal to g(n) and the notation is Big Omega**
* finite means either 0 or a non-zero constant
** nonzero means either a constant or infinity
--------------------------
| General Observations: |
--------------------------
* if f(n) is a polynomial in n of degree r, then f(n) is Big_Theta (n^r)
* if r < s then n^r is o(n^s)
* if a > 1 and b > 1 then log_a(n) is Big_Theta of (log_b(n))
* log n is o(n^r) for any r > 0
* for any real number a > 1, and any positive integer r, n^r is o(a^n)
* if 0 <= a < b then a^n is o(b^n)
* a^n is o(n!) for all a
You will not need calculus to determine limits but you will need a little creativity. For example, to find the limit as n->oo of f(n)/g(n), where f(n) = lg lgn and g(n) = lg n, replace lgn in f(n) with n. You know that lg (lg n) will never be greater than lg n, thus f(n) must be O(g(n)). Another trick, if you add functions such as x^3 + x^2, is to eliminate x^2 entirely since the growth rate of x^3 completely dominates the growth rate of x^2. You can likewise remove constant coefficients and constant terms.
Big-O Examples.
In the following list, f(n) comes before g(n) if f(n) is big-oh of (g(n)).
1. 100,000 4. n^0.1 7. n^2 2. lg lg n 5. n + lg n 8. n^3 + 100n^2 3. lg (n^3) 6. n lg n 9. 2^nBig-Theta Examples.
5000, 1 trillion , (any constant)
lg lg (n^2)
lg n, lg n^2
(lg n)^2 //f(10^2)=4 f(10^5)=25 f(10^6)=36
n^0.3 // f(10^2)=3.98 f(10^5)=32 f(10^6)=125; thus (lg n)^2 is o(n^.3)
n + lgn, sqrt(n^2 + 4), 4n + sqrt(n)
n^2 - 100n, n^2
n^2 lg n
n^3
2^n
3^n
n!
n^n
------------------------------------------------------------------------------
EXAMPLE 2.
Order the following functions into efficiency classes by ascending growth rate.
If two functions are big-theta of each other list them together.
1. 2000(n^1.5)
2. n^0.5 + log n
3. n log n^2n
4. log(log n)
5. n^2 + log n
6. log (300n^2)
7. n + (2000(log n))
8. (2^n)^2
9. 2^n(1.5)^n
First simplify functions by removing constants and terms of lower growth rate.
1. 2000(n^1.5) = n^1.5 // remove constant coefficient
2. n^0.5 + log n = n^0.5 // remove log n since n^0.5 dominates log n
3. n log n^2n = n log((n^n)(n^n))
= n(log(n^n)+log(n^n))
= 2n(log(n^n))
= 2n^2(log n)
= n^2 log n
4. log(log n) // nothing to do with this yet
5. n^2 + log n = n^2
6. log (300n^2) = log(300*n*n)
= log(300)+log(n)+log(n) // by rules of log arithmetic
= log(n)+log(n) //log(300) is a constant to eliminate it
= 2log(n)
= log(n) // 2 is a constant to eliminate it
7. n + 2000 log n = n // remove log n since n dominates log n
8. (2^n)^2 = 2^(2n)
9. 2.5^n
These are the functions we are left with:
n^1.5, n^.5, n^2 log n, log(log n), n^2, log n, n, 2^(2n), 2.5^n
Start grouping functions by smallest efficiency class first. Of those listed,
we know n dominates log n.
Does log n dominate log(log n)? Or is it big-theta of log(log n)? Finding the
ratio is difficult. We suspect that log(n) dominates log(log n) but we need to
prove it. Just looking at the graphs of both functions doesn't help a lot
either. We need to find some values for C and k to show that g(n) overtakes
f(n). Add some constant C to log(log n) to ensure that function starts below
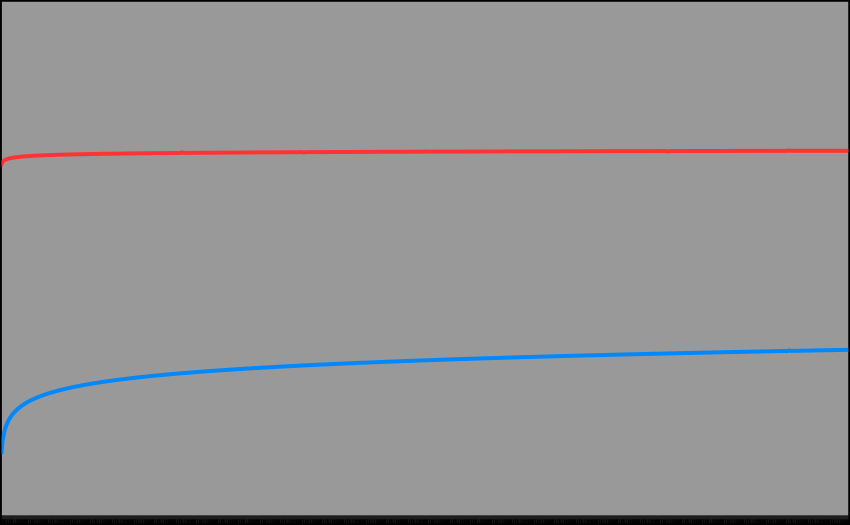
log n. C=5 works. This graph is from 1 to 10000 on the X axis.
The red line is
f(n)=5log(log(n)).
The blue line is
g(n)= log(n).
As you can see, it still is not clear that the blue line will ever overtake
the red line. We need to find a large value of n to show this.
For n = 100, f(n)=7.6 and g(n)=1. Off to a good start since f(n) at this
point is larger than g(n).
Now we just need to find some k such that g(k) > f(k).
Try k=10^20.
Let f(n) = 5log (log 10^20)
= 5log(20)
= 5*(1.3)
= 14.97
g(n) = log (10^20)
= 20. BINGO.
We now know that log(log n) is little-oh of log(n) since we found an n
such that log(n) overtook 5log(logn).
So we can continue arranging as follows:
n
log(log n)
log n
What about n^1.5 and n^.5?
We can find the ratio of these two functions:
n^1.5
n->oo ----- = n^1 // by rules of exponentiation
n^.5
The limit as n->oo of n is infinity we know that n^1.5 dominates n^.15.
Continuing:
n
log(log n)
log n
n^.5
n^1.5
n^2
n^2 log n
What about 2^(2n) and 2.5^n? Are they big-theta of each other?
We can find the ratio.
2^(2n) (2^n)(2^n)
n->oo ------ = ---------- // by rules of exponentiation
2.5^n (2^n)(.5^n)
= (2^n)/(.5^n)
= n
n->oo n = infinity.
Since the limit is infinity we know that 2^(2n) dominates 2.5^n.
FINAL ANSWER:
n
log(log n)
log n
n^.5
n^1.5
n^2
n^2 log n
2.5^n
2^(2n)